What is the Pythagorean Theorem And How is It Used in Measurement? Explained

The Pythagorean Theorem explains the relationship between the sides of a right triangle. It is a fundamental concept in geometry.

Named after the ancient Greek mathematician Pythagoras, the Pythagorean Theorem is a key principle in mathematics. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides.

This theorem is not just an abstract concept but has practical uses in various fields. From construction to navigation, it helps in accurately measuring distances. Understanding this theorem can simplify solving many real-world problems involving right triangles. In this blog post, we will explore the theorem in detail and see how it is applied in measurement.

Introduction To The Pythagorean Theorem

Hey friends, today we’re going to talk about something really cool and useful in math. It’s called the Pythagorean Theorem. This might sound a bit complex, but don’t worry. By the end of this post, you’ll understand what it is and how you can use it in measurements.

Historical Background

So, where did the Pythagorean Theorem come from? Good question. This theorem is named after a Greek mathematician named Pythagoras. Pythagoras lived a long time ago, around 500 BC. He and his followers studied numbers and shapes, and they discovered this special relationship in right-angled triangles.

Now, Pythagoras wasn’t the only one who knew about this theorem. Ancient Egyptians and Babylonians also used it, even before Pythagoras. But, he gets the credit because he proved it and made it famous.

Basic Concept

Alright, let’s get into the basic concept. The Pythagorean Theorem is all about right-angled triangles. You know, the ones with one angle that’s exactly 90 degrees. In such triangles, the longest side is called the hypotenuse. The other two sides are called the legs.

The theorem states that if you square the lengths of the two legs and add them together, you’ll get the square of the hypotenuse’s length. It’s written like this:

a2 + b2 = c2

Where:

• a is the length of one leg
• b is the length of the other leg
• c is the length of the hypotenuse

Simple, right? Let’s look at an example to make it clearer. Imagine you have a right-angled triangle with legs of 3 and 4 units. According to the theorem, the hypotenuse would be:

1. Square the lengths of the legs: 3² = 9 and 4² = 16
2. Add these squares: 9 + 16 = 25
3. Find the square root of the sum: √25 = 5

So, the hypotenuse is 5 units long. Easy peasy!

Now that you know the basics, you can start using the Pythagorean Theorem in real-life measurements. Whether you’re building something, playing sports, or just curious about triangles, this theorem is super handy. Stay tuned for more ways to use it in our next sections!

Credit: homework.study.com

Mathematical Formula

The Pythagorean Theorem is a fundamental principle in geometry. It helps in calculating the length of sides in right-angled triangles. This theorem has a straightforward mathematical formula.

Equation Description

The formula for the Pythagorean Theorem is a² + b² = c². In this equation, ‘a’ and ‘b’ represent the lengths of the two shorter sides of the triangle. ‘c’ is the length of the hypotenuse, the side opposite the right angle.

Key Components

Each part of the equation has a specific role. ‘a’ and ‘b’ are the legs of the triangle. They form the right angle. ‘c’ is the hypotenuse. It is always the longest side of the triangle. By knowing the lengths of any two sides, you can calculate the third.

Geometric Interpretation

The Pythagorean Theorem is a fundamental concept in geometry. It deals with the relationship between the sides of a right-angled triangle. This theorem is not just a mathematical formula. It is a visual and practical tool.

Understanding the geometric interpretation makes it easier to apply in real-life measurements. It helps in fields like construction, navigation, and art. Let’s delve into the key aspects of this theorem.

Right-angled Triangles

The Pythagorean Theorem applies to right-angled triangles. A right-angled triangle has one angle of 90 degrees. The longest side is called the hypotenuse. The other two sides are the legs.

The theorem states that the square of the hypotenuse equals the sum of the squares of the legs. In simple terms, if you know the lengths of two sides, you can find the third. This is crucial for accurate measurements.

Visual Representation

Visual representation helps in understanding the theorem better. Draw a right-angled triangle. Label the legs as ‘a’ and ‘b’. Label the hypotenuse as ‘c’. According to the theorem, a² + b² = c².

Imagine squares built on each side of the triangle. The area of the square on the hypotenuse is equal to the sum of the areas of the other two squares. This visual approach makes the concept clear and easy to remember.

Such visual aids are useful in teaching and practical applications. They help in solving problems and in understanding the relationships between different geometric shapes.

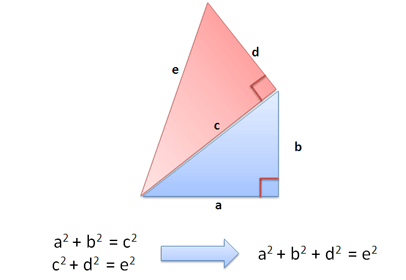
Credit: betterexplained.com

Applications In Real Life

The Pythagorean Theorem is not just for math class. It has many real-life applications. People use it to solve practical problems every day. Let’s explore how it helps in different fields.

Construction And Engineering

Builders use the Pythagorean Theorem to ensure structures are level and square. They measure the lengths of sides to create right angles. This is crucial for building homes, bridges, and roads. Engineers also use it in designing machinery and structures. Accurate measurements are essential for safety and efficiency.

Navigation And Mapping

Navigation relies on accurate distance measurement. The Pythagorean Theorem helps calculate the shortest path between two points. Sailors and pilots use it to navigate efficiently. It is also vital in mapping. Cartographers use it to measure distances on maps. This ensures that maps are accurate and useful for travel and planning.

Use In Measurement

The Pythagorean Theorem is a fundamental concept in geometry. It applies to right-angled triangles and states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. This theorem is not just a mathematical curiosity. It has practical applications in various fields, especially in measurement.

Distance Calculation

The Pythagorean Theorem helps calculate distances. Imagine you need to find the distance between two points on a map. These points form a right triangle with the grid lines. By knowing the lengths of the two shorter sides, you can use the theorem to find the hypotenuse. This hypotenuse represents the direct distance between the points.

Height And Depth Measurement

The theorem is also useful in measuring height and depth. Suppose you want to measure the height of a tree without climbing it. You can create a right-angled triangle with the tree and the ground. Measure the distance from the tree to a point on the ground. Then measure the angle from that point to the top of the tree. Using these measurements, apply the Pythagorean Theorem to calculate the tree’s height.

Similarly, it helps in measuring the depth of objects. For instance, to find the depth of a well, you can use the same principle. Measure the distance from the edge of the well to a point on the ground. Then measure the angle from that point to the bottom of the well. These measurements allow you to use the theorem to determine the well’s depth.

Examples And Practice Problems

The Pythagorean Theorem is a fundamental principle in geometry. It is used to find the length of a side in a right-angled triangle. Examples and practice problems can help you understand how to apply this theorem. By solving different problems, you can see how the theorem works in real-world situations.

Sample Problems

Let’s look at a few sample problems to practice the Pythagorean Theorem. Imagine you have a right-angled triangle with sides of lengths 3 and 4. What is the length of the hypotenuse? Another example is a triangle with sides of lengths 5 and 12. What is the hypotenuse length?

Step-by-step Solutions

To solve the first problem, use the Pythagorean Theorem formula: a² + b² = c². Here, a = 3 and b = 4. Plugging in these values, we get 3² + 4² = c². This simplifies to 9 + 16 = c², which means 25 = c². Taking the square root of both sides, c = 5.

For the second problem, a = 5 and b = 12. Using the formula, we have 5² + 12² = c². This means 25 + 144 = c². Simplifying further, 169 = c². The square root of 169 is 13, so c = 13.

These examples show how to apply the Pythagorean Theorem. Practice with more problems to get better.

Common Mistakes To Avoid

Hey friends, today we’re diving into some common mistakes people make when using the Pythagorean Theorem. It’s a powerful tool for measurement, but it’s easy to slip up if you’re not careful. Let’s break it down together.

Calculation Errors

First up, calculation errors. It’s a big one. Imagine you’re baking a cake. You mix all the ingredients, but forget the sugar. What happens? The cake flops. The same goes for the Pythagorean Theorem. If you mess up your calculations, your results will be off.

• Double-check your numbers. Always.
• Use a calculator if you’re unsure.
• Practice makes perfect. The more you use it, the better you’ll get.

Once, I was helping my nephew with his homework. We were working on a triangle problem. We got the sides mixed up and ended with a wrong answer. Lesson learned: Pay attention to details.

Misinterpretation Of Data

The next mistake is misinterpreting data. It’s like reading a map upside down. You won’t get where you want to go. Here’s a simple tip to avoid this.

1. Identify the sides correctly. Remember, a and b are the legs, and c is the hypotenuse.
2. Check your triangle. Make sure it’s a right triangle.
3. Review your problem. Ensure you understand what’s being asked.

Think of it like making a puzzle. If the pieces don’t fit, the picture won’t look right. Stay focused, and don’t rush. I once assumed a triangle was right-angled without checking. Big mistake! My whole solution was wrong.

The good news? Avoiding these mistakes is simple. Just take your time and follow these steps. Happy measuring!

Credit: www.chegg.com

Advanced Uses

The Pythagorean Theorem is more than a basic math concept. It finds advanced applications in various fields, helping solve complex problems. Here, we will explore its advanced uses in different areas of mathematics.

Trigonometry

The Pythagorean Theorem plays a key role in trigonometry. It helps find the lengths of sides in right triangles. This theorem is crucial for defining trigonometric ratios. These ratios include sine, cosine, and tangent. They are essential for solving real-world problems in physics and engineering. For example, it is used to calculate the height of a building or the distance between two points.

Analytical Geometry

In analytical geometry, the Pythagorean Theorem helps find distances between points. It is used in the distance formula. This formula calculates the distance between two points in a plane. The theorem also assists in defining the equation of a circle. Knowing the radius and center, one can easily plot the circle. This application is vital in computer graphics and design.

Frequently Asked Questions

What Is The Pythagorean Theorem Measurement?

The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. The formula is \(a^2 + b^2 = c^2\).

What Is Pythagorean Theorem And How Do You Use It?

The Pythagorean theorem states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. Use it by applying the formula: \(a^2 + b^2 = c^2\), where \(c\) is the hypotenuse.

What Is The Pythagoras Theorem?

The Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides.

How To Use Pythagorean Theorem To Find Distance?

Use the Pythagorean theorem to find distance by squaring the differences in x and y coordinates. Add them, then take the square root. The formula is: distance = √((x2 – x1)² + (y2 – y1)²). This method works for finding distance between two points in a plane.

Conclusion

The Pythagorean Theorem is a key tool in measurement. It helps find distances and calculate areas. Builders use it for accurate construction. Surveyors rely on it for mapping. Students learn it to understand geometry better. It’s a simple yet powerful formula.

Always remember, a² + b² = c². This theorem makes many tasks easier. So next time, apply it confidently!