How to Calculate the Area of a Triangle Using Angles? Expert Guide

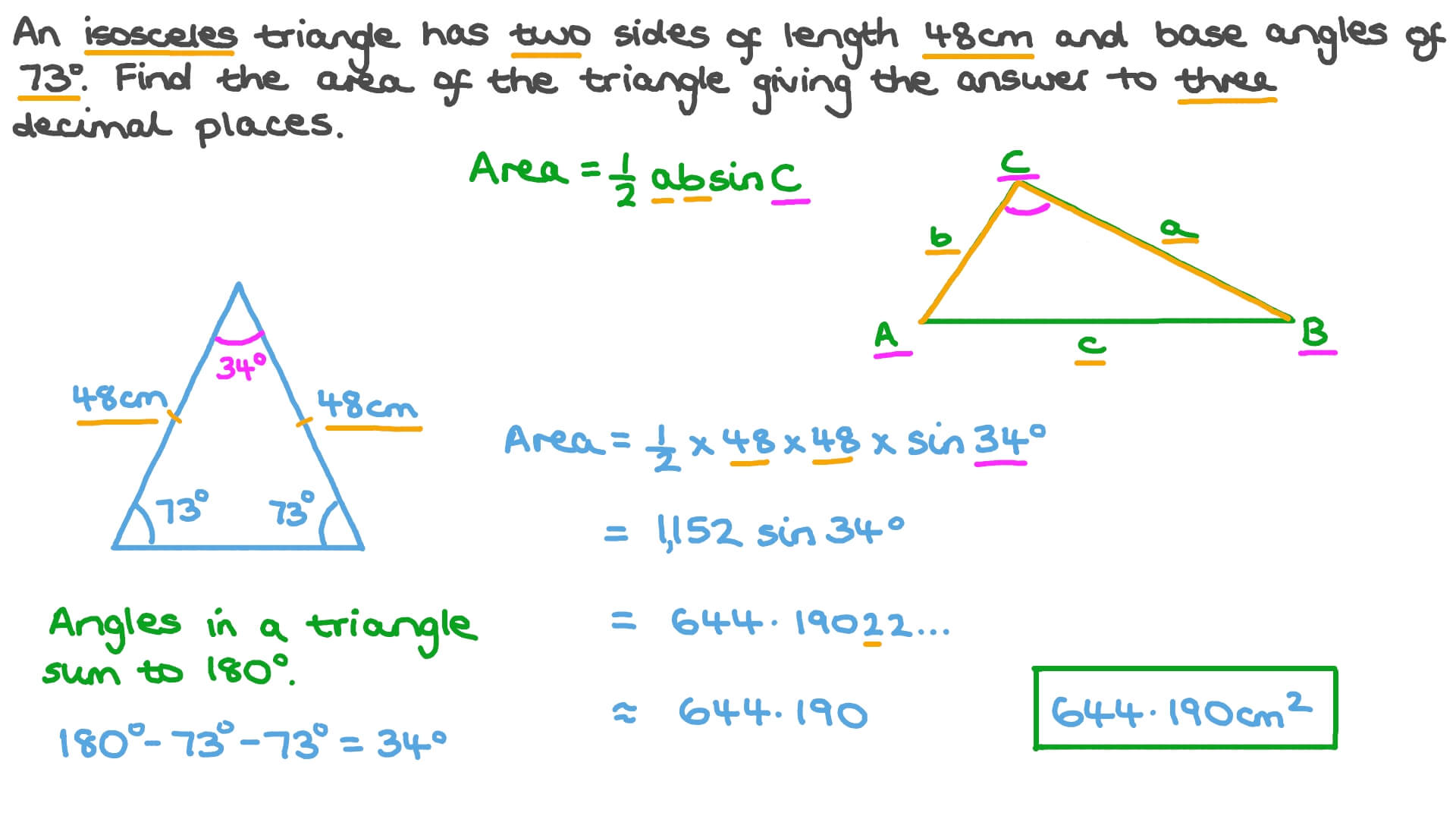
To calculate the area of a triangle using angles, you need to know two sides and the included angle. Once you have these values, you can apply a simple formula.

Triangles are fundamental shapes in geometry, and knowing how to find their area is essential. While many learn the basic formula (base times height divided by two), there’s another method that uses angles. This method is particularly useful in trigonometry and real-world applications.

Understanding it adds to your mathematical toolkit, making it easier to solve various problems. So, let’s dive into the process of calculating the area of a triangle using angles. This approach will help you solve geometry problems more efficiently and enhance your overall math skills.

Credit: www.nagwa.com

Basic Concepts

Hey there! Want to learn how to calculate the area of a triangle using angles? It’s simpler than you might think. Let’s break down the basic concepts you need to know. Understanding these will make the process much easier. Ready? Let’s dive in!

Understanding Triangle Properties

First, let’s talk about the properties of a triangle. A triangle is a shape with three sides and three angles. The sum of the angles in any triangle is always 180 degrees. This is a key fact to remember.

Imagine a triangle as a slice of pizza. The crust is one side, and the other two edges meet at a point, forming the angles. Knowing the properties helps us understand how to calculate the area.

Key Angles And Sides

Next, let’s identify the key angles and sides. There are different types of triangles, but for calculating the area using angles, we often use:

• Two sides of the triangle
• The angle between those two sides

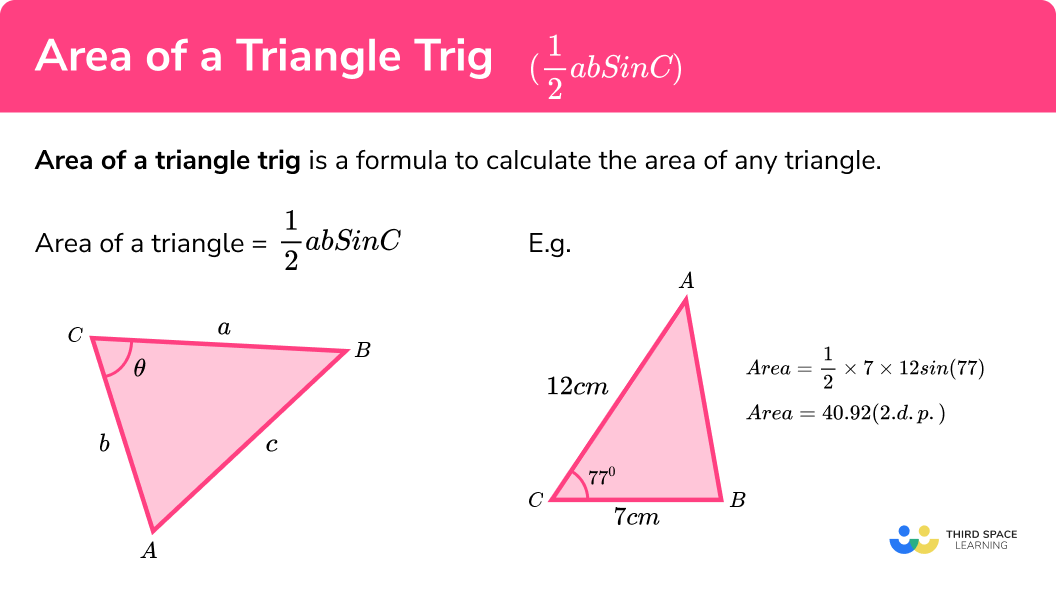
Think of it like this: if you have a triangle with sides a and b, and the angle between them is θ, you can use a special formula to find the area. This formula is:

Area = 1/2 a b sin(θ)

Here’s an example. Imagine you have a triangle with sides of 5 cm and 7 cm, and the angle between them is 30 degrees. Plug these values into the formula, and you can find the area easily.

That’s pretty much it! By understanding these basic concepts, calculating the area of a triangle using angles becomes a piece of cake. Stay tuned for more tips and tricks on mastering this topic.

Credit: thirdspacelearning.com

Formulas For Area Calculation

Hey friends! Today, we’re diving into some handy math formulas. We’ll learn how to calculate the area of a triangle using angles. Sounds tricky? Don’t worry, it’s easier than you think. We’ll break it down step-by-step and keep it simple. Ready? Let’s get started with the formulas for area calculation.

Sine Rule

First up, the Sine Rule. This one is pretty cool. It uses the sine of an angle to find the area. Here’s how it works:

• Imagine your triangle has sides a, b, and c.
• And the angles opposite these sides are A, B, and C.

The formula is:

Area = 0.5 a b sin(C)

Let’s break it down:

1. Pick two sides, say a and b.
2. Find the sine of the angle between them, which is C.
3. Multiply the lengths of the sides (a and b).
4. Multiply this result by the sine of angle C.
5. Finally, multiply by 0.5. That’s it!

Example time! Suppose a = 5, b = 7, and angle C = 30 degrees. Plug them into the formula:

Area = 0.5 5 7 sin(30)

The sine of 30 degrees is 0.5. So,

Area = 0.5 5 7 0.5 = 8.75 square units.

See? Not so hard!

Cosine Rule

Next, the Cosine Rule. This one is a bit different but just as useful. Here’s the formula:

Area = 0.5 a b sin(C)

Wait a minute. Isn’t this the same as the Sine Rule? Yes, it is! The Cosine Rule is mainly used for finding the sides or angles, not directly for area. But you can use the cosine rule to find an angle first, and then use the sine rule to find the area.

Here’s how:

1. Use the Cosine Rule to find an angle if you know all three sides. The formula is:
• c² = a² + b² – 2abcos(C)
2. Rearrange to find cos(C):
• cos(C) = (a² + b² – c²) / (2ab)
3. Find the angle C by taking the inverse cosine (arccos).
4. Now, use this angle in the Sine Rule to find the area.

Let’s try an example. Suppose a = 6, b = 8, and c = 10. First, find angle C:

cos(C) = (6² + 8² – 10²) / (2 6 8)

That’s cos(C) = (36 + 64 – 100) / 96 = 0 / 96 = 0

So, cos(C) = 0. The angle C is 90 degrees because the cosine of 90 degrees is 0.

Now use the Sine Rule:

Area = 0.5 6 8 sin(90)

Since sin(90) is 1, the area is:

Area = 0.5 6 8 1 = 24 square units.

And there you have it! Using these simple steps, you can calculate the area of any triangle using angles. Try it out, and you’ll see how easy it can be.

Using The Sine Formula

Calculating the area of a triangle can be simple with the right tools. One effective method is using the sine formula. This method requires knowing two sides and the included angle. It is especially useful when dealing with non-right triangles. Let’s dive into the details.

Step-by-step Guide

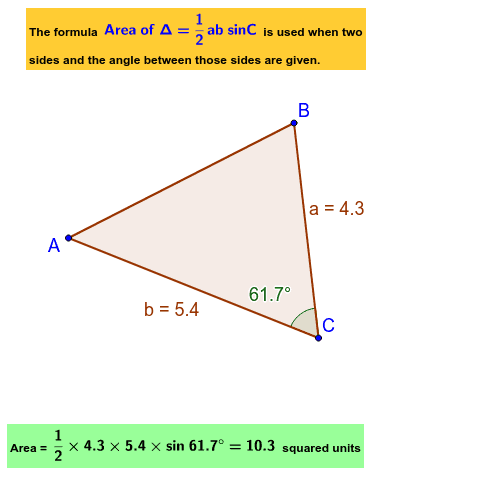
First, identify the sides and the included angle. Label the sides as “a” and “b”. The included angle should be “C”. The formula to find the area is: (1/2) a b sin(C).

Next, measure the sides “a” and “b”. Ensure the measurements are accurate. Also, measure the angle “C” in degrees. Convert the angle into radians if needed. Many calculators have a sine function for this conversion.

Then, plug the values into the formula. Multiply the sides “a” and “b”. Find the sine of angle “C”. Multiply this result by 0.5. The final value is the area of the triangle.

Example Calculation

Let’s consider an example. Suppose we have a triangle with sides a = 5 units and b = 7 units. The included angle C is 45 degrees.

First, convert the angle into radians if needed. Use the calculator to find sin(45 degrees). The sine of 45 degrees is approximately 0.707.

Next, apply the formula: (1/2) 5 7 0.707. Multiply 5 by 7 to get 35. Then multiply 35 by 0.707 to get 24.745. Finally, multiply by 0.5. The area of the triangle is approximately 12.37 square units.

Applying The Cosine Formula

Hey friends, today I’ll show you how to find the area of a triangle using the cosine formula. This method is super handy, especially when you know the lengths of all three sides but none of the heights. It’s a bit of math magic! So, let’s dive in and make it easy to understand.

Step-by-step Guide

First things first. To calculate the area of a triangle using angles, we will use the cosine formula. Here’s the step-by-step guide:

1. Identify the sides of the triangle. Let’s call them a, b, and c.
2. Determine the angle between sides a and b. Let’s call this angle θ.
3. Use the cosine formula to find the area. The formula is:
   Area = 0.5 a b sin(θ)

Sounds complicated? Don’t worry. Let’s break it down with an example.

Example Calculation

Imagine we have a triangle with sides a = 5, b = 7, and the angle between them θ = 60°. Here’s how you calculate the area:

1. Identify the sides: a = 5 and b = 7.
2. Identify the angle: θ = 60°.
3. Plug these values into the formula:
   Area = 0.5 5 7 sin(60°)
4. Calculate the sine of 60°. You can use a calculator for this:
   sin(60°) ≈ 0.866
5. Now, multiply these values:
   Area ≈ 0.5 5 7 0.866
6. Finally, calculate the result:
   Area ≈ 15.155

So, the area of the triangle is approximately 15.155 square units. Easy, right?

Remember, practice makes perfect. Try using this method with different values and see how it works. Pretty soon, you’ll be a pro at calculating the area of triangles using the cosine formula!

Special Cases

Hey friends, today we are diving into some special cases for calculating the area of a triangle using angles. Sometimes, you get a triangle that fits into a special category, and that can make your calculations easier. Let’s look at how to handle two common types: right-angled triangles and equilateral triangles.

Right-angled Triangles

Right-angled triangles are pretty common in geometry. A right-angled triangle has one angle that’s exactly 90 degrees. This special angle makes our job simpler. Why? Because we can use a formula that’s specifically for right-angled triangles.

Here’s how you do it:

1. Identify the two sides that make the right angle. These are called the base and the height.
2. Use the formula: Area = 1/2 base height

Let’s say you have a right-angled triangle where the base is 4 units and the height is 3 units. Your calculation will look like this:

Area = 1/2 4 3 = 6 square units

Easy, right? Just remember, for right-angled triangles, you don’t need to worry about the angles too much. Focus on the base and height.

Equilateral Triangles

Equilateral triangles are also special. All three sides are the same length, and all three angles are 60 degrees. This symmetry helps us use a neat formula to find the area.

Here’s what you do:

1. Measure one side of the triangle. We’ll call this the side length.
2. Use the formula: Area = (sqrt(3)/4) side^2

For example, if your equilateral triangle has sides of 5 units, your calculation will be:

Area = (sqrt(3)/4) 5^2 ≈ 10.83 square units

This formula works every time for equilateral triangles. No need to mess around with different angles or heights.

So, there you have it! Two special cases for calculating the area of triangles using angles. Whether it’s a right-angled triangle or an equilateral triangle, these formulas make your life easier. Remember these tips, and you’ll solve these problems quickly and accurately. Happy calculating!

Credit: www.geogebra.org

Common Mistakes To Avoid

Calculating the area of a triangle using angles can be tricky. Many make mistakes that lead to incorrect results. Knowing these common mistakes can help avoid errors and ensure accurate calculations.

Incorrect Angle Measurement

One common mistake is incorrect angle measurement. Always measure angles accurately. Even a small error can lead to wrong area calculations. Use a protractor or digital angle finder for precision. Double-check measurements to avoid mistakes.

Misapplication Of Formulas

Another mistake is the misapplication of formulas. Ensure you use the correct formula for the given problem. For triangles, the formula often involves sine or cosine. Using the wrong formula can result in incorrect answers. Understand each formula and its application before using it.

Practical Applications

Hey friends, ever wondered why you need to know how to calculate the area of a triangle using angles? Well, it’s not just for math class. This skill has many practical uses in everyday life. Let’s dive into some real-world examples and understand its importance in various fields.

Real-world Examples

Imagine you are designing a piece of land for a new garden. You need to figure out how much space you have. Knowing how to calculate the area of a triangle can help. Or think about building a treehouse. You need to know the space available to ensure it’s safe and sturdy.

Here are some common scenarios:

• Landscaping: Planning a new garden layout.
• Construction: Building houses, sheds, or treehouses.
• Art and Design: Creating geometric shapes in artwork.

Importance In Various Fields

So, why is this important? Because it’s used in many fields:

• Engineering: Engineers use this calculation to design and build structures.
• Architecture: Architects need to know the areas of different shapes for designing buildings.
• Geography: Geographers calculate land areas to study regions.

Even in everyday tasks, knowing these calculations can come in handy. For example, I recently needed to calculate the space for a new bookshelf. Knowing how to use angles to find the area helped me make the best use of my room space.

And the best part? These calculations aren’t as hard as they seem. Once you get the hang of it, you’ll find it easier to solve many practical problems. So, keep practicing, and soon you’ll see how useful this skill is in real life!

Frequently Asked Questions

What Is The Formula For The Area Of A Triangle Using Angles?

The formula for the area of a triangle using angles is: 0. 5 * a * b * sin(C). Here, a and b are sides, and C is the included angle between them.

Can You Solve A Triangle With Only Angles?

No, you cannot solve a triangle with only angles. You need at least one side length to determine the triangle’s dimensions.

How To Calculate The Area Of A Triangle?

To calculate the area of a triangle, use the formula: 0. 5 * base * height. Measure the base and height perpendicularly. Multiply them and divide by two.

How To Find Area Of Triangle With Side Angle Side?

To find the area of a triangle with side-angle-side, use the formula: (1/2) * a * b * sin(C). Here, “a” and “b” are the lengths of the sides, and “C” is the included angle.

Conclusion

Calculating the area of a triangle using angles is straightforward. Follow the formula and steps discussed. Practice will make you more confident. Always double-check your work to avoid errors. Understanding this method helps in geometry problems. With clear explanations and simple steps, you can tackle any triangle area challenge.

Keep practicing and soon it will feel natural. Remember, math skills improve with consistent effort. Happy calculating!